Contoh soal penggunaan integral tentu untuk menghitung luas daerah.
Jika kamu mencari artikel contoh soal penggunaan integral tentu untuk menghitung luas daerah terlengkap, berarti kamu telah berada di blog yang tepat. Yuk langsung aja kita simak penjelasan contoh soal penggunaan integral tentu untuk menghitung luas daerah berikut ini.
Menghitung Luas Daerah Menggunakan Integral From utakatikotak.com
Batasnya adalah dari y 1 sampai y 4. Perhatikanlah ilustrasi jika suatu bidang datar dirotasikan terhadap sumbu Y. Hampir semua benda tiga dimensi yang kita sentuh dan lihat merupakan hasil perputaran suatu permukaan mengelilingi suatu patokan garis. Jelasnya berikut adalah contoh soal integral luas derah beserta pembahasannya.
7 8 9 10 11 12 Menggunakan integral untuk menghitung luas daerah dibawah kurva from ACCOUNTING 0819114186 at Universitas Negeri Jakarta.
Contoh Soal Dan Pembahasan Integral Tentu Untuk Menghitung. Luas daerahnya adalah 2 23 satuan luas. Yx2-1 x1 dan xp p0 adalah 43 tentukan nilai p. Sebagai contoh tabung merupakan hasil perputaran persegi panjang mengelilingi sumbu tegak sejauh 360. Jika dilihat dari parabola y 2x 2 8x 6 daerah yang diarsir ada yang di bawah parabola dan dan di atas parabola.
Source: madematika.net
Batasnya adalah dari y 1 sampai y 4. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu Y. Fungsinya adalah y 4 - x2 rightarrow x sqrt4 - y. Fungsinya adalah y 4 x2 rightarrow x sqrt 4 y. Batasnya adalah dari y 1 sampai y 4.
Persamaan parabola yang memotong sumbu-x di titik 0 0 dan 5 0 dan melalui titik 1 4 adalah.
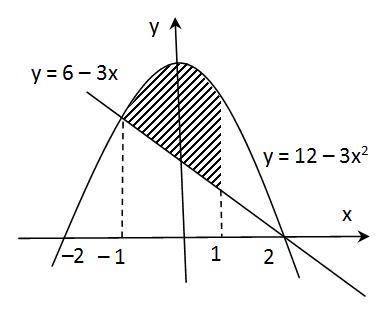
Luas Daerah yang Dibatasi Kurva Untuk menghitung luas daerah yang dibatasi suatu kurva dengan sumbu x dapat kita gunakan konsep integral tentu Perhatikan Ilustrasi berikut. Batasnya adalah dari y 1 sampai y 4. Perhatikan bahwa dari selang 0 4 kurva y 6 x x 2 selalu berada di atas kurva y x 2 2 x. Kumpulan Contoh Soal Dan Pembahasan Integral Tentu Untuk Menghitung Luas Daerah Pembahasan.
Source: id.pinterest.com
Jika dilihat dari parabola y 2x 2 8x 6 daerah yang diarsir ada yang di bawah parabola dan dan di atas parabola. Integral Tak Tentu dan Luas Daerah. Y 2x 5 dan sumbu x. Kumpulan Contoh Soal Dan Pembahasan Integral Tentu Untuk Menghitung Luas Daerah Pembahasan.
Source: madematika.net
Batasnya adalah dari y 1 sampai y 4. Integral Tak Tentu dan Luas Daerah. Batasnya adalah dari y 1 sampai y 4. Untuk menghitung luasnya masing-masing harus dihitung sendiri.
Source: teamhannamy.blogspot.com
Luas Daerah yang Dibatasi Kurva Untuk menghitung luas daerah yang dibatasi suatu kurva dengan sumbu x dapat kita gunakan konsep integral tentu Perhatikan Ilustrasi berikut. Oleh karena itu untuk mengerjakan soal mengenai luas daerah otakers perlu menggunakan konsep integral tak tentu. Jika dilihat dari parabola y 2x 2 8x 6 daerah yang diarsir ada yang di bawah parabola dan dan di atas parabola. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu Y.
Untuk menghitung luasnya masing-masing harus dihitung sendiri. Menentukan Batas Jika Diketahui Luasnya. Luas daerah yang dibatasi oleh y 2x 2 8x 6 y 2x 2 x 1 dan x 4 adalah. Hitunglah luas daerah yang dibatasi oleh garis y x.
Oleh karena itu untuk mengerjakan soal mengenai luas daerah otakers perlu menggunakan konsep integral tak tentu.
Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu y. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu Y. Kumpulan Contoh Soal Dan Pembahasan Integral Tentu Untuk Menghitung Luas Daerah Pembahasan. Soal dan Pembahasan Volume Benda Putar Menggunakan Integral. Volume Benda Putar.
Source: kompas.com
Luas daerahnya adalah 2 23 satuan luas. Hitunglah luas daerah yang dibatasi oleh garis y x. Jadi luas daerahnya adalah 1 78 satuan luas. Perhatikanlah ilustrasi jika suatu bidang datar dirotasikan terhadap sumbu Y. Contoh Soal Dan Pembahasan Integral Tentu Untuk Menghitung.
Selama kita dapat menyatakan sisi. Menentukan Batas Jika Diketahui Luasnya. Hitunglah luas daerah yang dibatasi oleh kurva x 2 6x dan sumbu x dari -6 hingga 0. Aplikasi integral yang biasanya dipelajari adalah penerapan integral dalam menghitung luas daerah yang dibatasi oleh kurva dan penggunaan integral untuk menentukan volume benda putar.
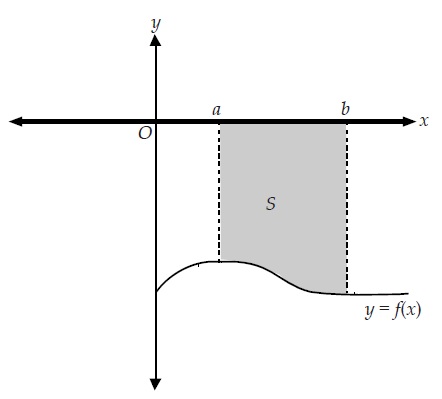
Luas Daerah yang Dibatasi Kurva Untuk menghitung luas daerah yang dibatasi suatu kurva dengan sumbu x dapat kita gunakan konsep integral tentu Perhatikan Ilustrasi berikut.
Jelasnya berikut adalah contoh soal integral luas derah beserta pembahasannya. Fungsinya adalah y 4 x2 rightarrow x sqrt4 y. Dengan demikian luasnya dapat ditentukan dengan menggunakan integral tentu berikut. Tentukan luas untuk setiap daerah arsiran berikut.
Source: teamhannamy.blogspot.com
Hitunglah luas daerah yang dibatasi oleh kurva x 2 6x dan sumbu x dari -6 hingga 0. Yx2-1 x1 dan xp p0 adalah 43 tentukan nilai p. Contoh Soal Dan Pembahasan Integral Tentu Untuk Menghitung. Hitunglah luas daerah yang dibatasi oleh garis y x.
Source: slidetodoc.com
Jelasnya berikut adalah contoh soal integral luas derah beserta pembahasannya. Dengan demikian luasnya dapat ditentukan dengan menggunakan integral tentu berikut. Contoh Soal Dan Pembahasan Integral Tentu Untuk Menghitung. Luas daerah yang dibatasi oleh kurva f x x 2 2x 3 dan g x 3 x adalah.
Source: teamhannamy.blogspot.com
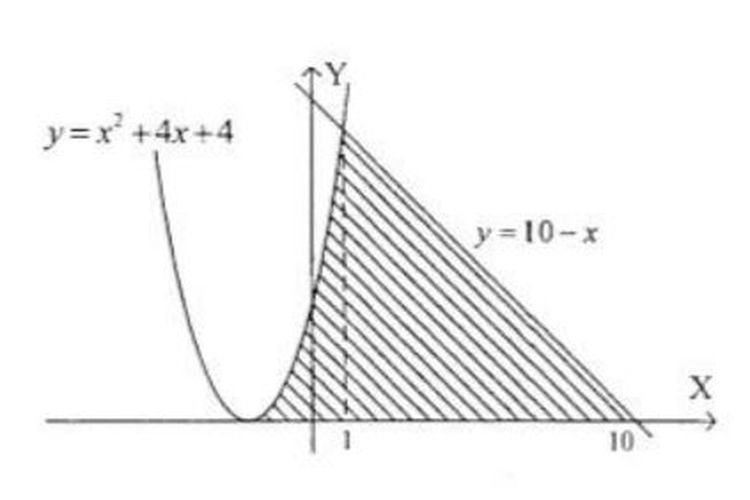
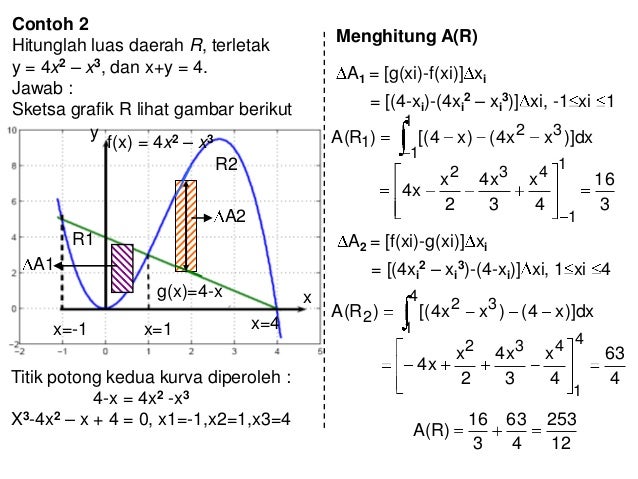
Untuk itu kita harus menghitung 2 kali pertama yang di bawah. Contoh 1 Aplikasi Integral untuk menghitung luas daerah yang dibatasi kurva. Contoh lain untuk tipe soal yang dapat menggunakan rumus cepat menghitung luas daerah yang dibatasi integral adalah sebagai berikut. Fungsinya adalah y 4 x2 rightarrow x sqrt4 y.
Luas Daerah yang Dibatasi Kurva Untuk menghitung luas daerah yang dibatasi suatu kurva dengan sumbu x dapat kita gunakan konsep integral tentu Perhatikan Ilustrasi berikut.
Soal dan Pembahasan Volume Benda Putar Menggunakan Integral. Jika dilihat dari parabola y 2x 2 8x 6 daerah yang diarsir ada yang di bawah parabola dan dan di atas parabola. Untuk menghitung luasnya masing-masing harus dihitung sendiri. Daerah yang diarsir dibatasi oleh dua kurva parabola yaitu y x 2 2 x dan y 6 x x 2. Hitunglah luas daerah yang dibatasi oleh kurva x 2 6x dan sumbu x dari -6 hingga 0.
Source: contohsoaldanmateripelajaran-211.blogspot.com
8 contoh soal dan pembahasan integral. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu Y. Y 2x 5 dan sumbu x. Yx2-1 x1 dan xp p0 adalah 43 tentukan nilai p. Contoh 1 Aplikasi Integral untuk menghitung luas daerah yang dibatasi kurva.
Untuk menghitung luasnya masing-masing harus dihitung sendiri.
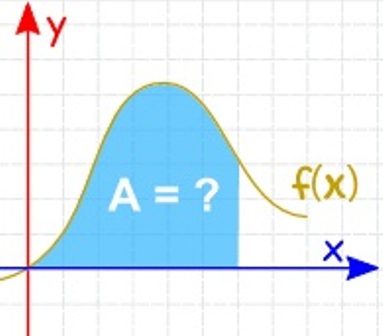
8 contoh soal dan pembahasan integral. Misalkan kita diberikan gambar berikut maka luas adalah. Batasnya adalah dari y 1 sampai y 4. Selama kita dapat menyatakan sisi.
Source: contohsoaldanmateripelajaran-211.blogspot.com
Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu y. Perhatikan bahwa dari selang 0 4 kurva y 6 x x 2 selalu berada di atas kurva y x 2 2 x. Jelasnya berikut adalah contoh soal integral luas derah beserta pembahasannya. Sebagai contoh tabung merupakan hasil perputaran persegi panjang mengelilingi sumbu tegak sejauh 360.
Source: teamhannamy.blogspot.com
Jika anda telah memahami konsep dasar integral yaitu integral tak tentu dan integral tentuAnda akan mungkin lebih mudah dalam mempelajari aplikasi dari integral. Jika dilihat dari parabola y 2x 2 8x 6 daerah yang diarsir ada yang di bawah parabola dan dan di atas parabola. Luas daerah yang dibatasi oleh y 2x 2 8x 6 y 2x 2 x 1 dan x 4 adalah. Persamaan parabola yang memotong sumbu-x di titik 0 0 dan 5 0 dan melalui titik 1 4 adalah.
Source: encrypted-tbn0.gstatic.com
Selama kita dapat menyatakan sisi. Contoh 1 Aplikasi Integral untuk menghitung luas daerah yang dibatasi kurva. Soal dan Pembahasan Volume Benda Putar Menggunakan Integral. Volume Benda Putar.
Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu y.
Fungsinya adalah y 4 x2 rightarrow x sqrt4 y. Sebagai contoh tabung merupakan hasil perputaran persegi panjang mengelilingi sumbu tegak sejauh 360. Luas daerahnya adalah 2 23 satuan luas. Contoh lain untuk tipe soal yang dapat menggunakan rumus cepat menghitung luas daerah yang dibatasi integral adalah sebagai berikut. Tentukan luas untuk setiap daerah arsiran berikut.
Source: kompas.com
Kumpulan Contoh Soal Dan Pembahasan Integral Tentu Untuk Menghitung Luas Daerah Pembahasan. Y 2x 5 dan sumbu x. Dengan demikian luasnya dapat ditentukan dengan menggunakan integral tentu berikut. Aplikasi integral yang biasanya dipelajari adalah penerapan integral dalam menghitung luas daerah yang dibatasi oleh kurva dan penggunaan integral untuk menentukan volume benda putar. Luas daerah yang dibatasi oleh kurva f x x 2 2x 3 dan g x 3 x adalah.
Hitunglah luas daerah yang dibatasi oleh garis y x.
Fungsinya adalah y 4 x2 rightarrow x sqrt 4 y. Menentukan luas daerah di bawah sumbu x. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu y. Luas daerah yang dibatasi oleh y 2x 2 8x 6 y 2x 2 x 1 dan x 4 adalah.
Source: contohsoaldanmateripelajaran-211.blogspot.com
Volume Benda Putar. Jika dilihat dari parabola y 2x 2 8x 6 daerah yang diarsir ada yang di bawah parabola dan dan di atas parabola. Dengan demikian luasnya dapat ditentukan dengan menggunakan integral tentu berikut. Volume Benda Putar. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu Y.
Source: teamhannamy.blogspot.com
Perhatikan bahwa dari selang 0 4 kurva y 6 x x 2 selalu berada di atas kurva y x 2 2 x. 7 8 9 10 11 12 Menggunakan integral untuk menghitung luas daerah dibawah kurva from ACCOUNTING 0819114186 at Universitas Negeri Jakarta. Contoh 1 Aplikasi Integral untuk menghitung luas daerah yang dibatasi kurva. Fungsinya adalah y 4 x2 rightarrow x sqrt 4 y. Selama kita dapat menyatakan sisi.
Source: slideshare.net
Fungsinya adalah y 4 x2 rightarrow x sqrt4 y. Misalkan kita diberikan gambar berikut maka luas adalah. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu Y. Contoh lain untuk tipe soal yang dapat menggunakan rumus cepat menghitung luas daerah yang dibatasi integral adalah sebagai berikut. Daerah yang diarsir dibatasi oleh dua kurva parabola yaitu y x 2 2 x dan y 6 x x 2.
Situs ini adalah komunitas terbuka bagi pengguna untuk membagikan apa yang mereka cari di internet, semua konten atau gambar di situs web ini hanya untuk penggunaan pribadi, sangat dilarang untuk menggunakan artikel ini untuk tujuan komersial, jika Anda adalah penulisnya dan menemukan gambar ini dibagikan tanpa izin Anda, silakan ajukan laporan DMCA kepada Kami.
Jika Anda menemukan situs ini baik, tolong dukung kami dengan membagikan postingan ini ke akun media sosial seperti Facebook, Instagram dan sebagainya atau bisa juga simpan halaman blog ini dengan judul contoh soal penggunaan integral tentu untuk menghitung luas daerah dengan menggunakan Ctrl + D untuk perangkat laptop dengan sistem operasi Windows atau Command + D untuk laptop dengan sistem operasi Apple. Jika Anda menggunakan smartphone, Anda juga dapat menggunakan menu laci dari browser yang Anda gunakan. Baik itu sistem operasi Windows, Mac, iOS, atau Android, Anda tetap dapat menandai situs web ini.
