Contoh soal integral tentu menghitung luas daerah.
Jika kamu mencari artikel contoh soal integral tentu menghitung luas daerah terlengkap, berarti kamu telah berada di web yang benar. Yuk langsung saja kita simak pembahasan contoh soal integral tentu menghitung luas daerah berikut ini.
Integral Tentu Penggunaan Integral Materi Rumus Contoh Soal From studiobelajar.com
Perhatikan bahwa dari selang 0 4 kurva y 6 x x 2 selalu berada di atas kurva y x 2 2 x. Hitunglah luas daerah yang dibatasi oleh kurva y x - 2x dan sumbu x. Menentukan Batas Jika Diketahui Luasnya. Luas daerah yang dibatasi oleh kurva y x 2 4x 5 dan sumbu x adalah.
Luas daerah yang diarsir pada gambar di atas dapat dinyatakan dengan rumus.
Luas daerah yang dibatasi oleh kurva yx² dan garis xy6 adalah. Dengan demikian luasnya dapat ditentukan dengan menggunakan integral tentu berikut. Berikut ini contoh integral luas daerah di bawah sumbu x beserta pembahasanya. Berdasarkan soal tersebut dapat kita lihat bahwa hanya terdapat satu titik potong yaitu. Agar kita dapat melihat perbedaan soal 1 dan soal 2.
Source: encrypted-tbn0.gstatic.com
Dengan demikian luasnya dapat ditentukan dengan menggunakan integral tentu berikut. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu y. Luas daerah yang dibatasi oleh kurva y x 2 4x 5 dan sumbu x adalah. L 10 3 10 3. Perhatikan bahwa dari selang 0 4 kurva y 6 x x 2 selalu berada di atas kurva y x 2 2 x.
Selanjutnya kita akan menghitung luas daerah tersebut dengan batas a 3 dan b 0.
Kumpulan Contoh Soal Dan Pembahasan Integral Tentu Untuk Menghitung Luas Daerah Pembahasan January 19 2021 by admin Jelasnya berikut adalah contoh soal integral luas derah beserta pembahasannya. Berdasarkan soal tersebut dapat kita lihat bahwa hanya terdapat satu titik potong yaitu. Integral Tak Tentu dan Luas Daerah. L 1 3x3 3 2x22 0 1 3 x 3 3 2 x 2 0 2.
Source: slideshare.net
Jadi luas daerahnya adalah 1 78 satuan luas. Contoh 2 Aplikasi Integral Menghitung Luas Daerah yang Dibatasi Kurva. Untuk itu kita harus menghitung 2 kali pertama yang di bawah parabola dan kedua yang dibawah parabola. Rumus Cepat Menghitung Luas Daerah yang Dibatasi Kurva.
Source: studiobelajar.com
Integral banyak sekali penggunaanya seperti dalam menghitung luas daerah dibidang datar menggunakan integralmenghitung panjang busur menghitung luas selimut benda putar menghitung volume benda putar Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva di bawah kurva di atas sumbu x ataupun di bawah sumbu x. Menggunakan integral untuk mencari luas daerah yang dibatasi oleh dua kurvaCara cepatnya bisa dilihat di sinihttpsyoutubeoSmJaXXDTQE. Salah satu aplikasi integral adalah untuk menghitung luas bidang datar yang dibentuk oleh persamaan-persamaan garis atau kurva. Misalkan persamaan garis kita tulis menjadi.
Source: idschool.net
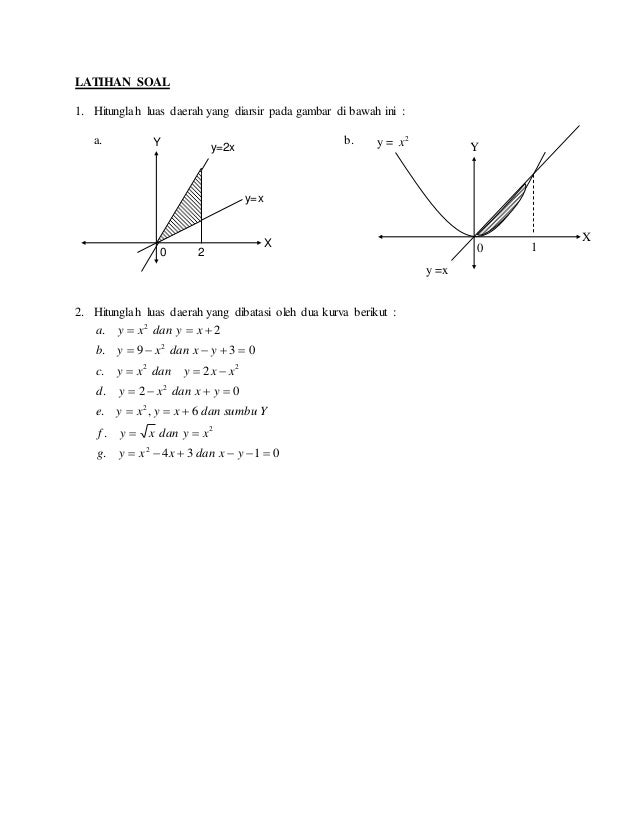
Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu Y. Pada bagian yang diarsir kurva fx lebih di atas dibandingkan dengan kurva gx maka luas daerah di atas bisa dinyatakan dengan contoh soal 5. Hitunglah luas daerah yang dibatasi oleh garis y x. Menentukan Batas Jika Diketahui Luasnya.
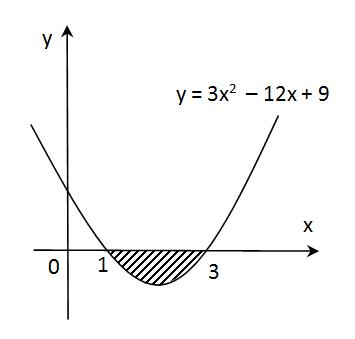
Luas daerahnya adalah 2 23 satuan luas. Luas daerah yang dibatasi oleh kurva y x 2 4x 5 dan sumbu x adalah. Menentukan luas daerah di bawah sumbu x. Sumbu x berarti garis y 0.
Sebuah daerah dibatasi oleh persamaan y 2 x dan y x 2.
Untuk itu kita harus menghitung 2 kali pertama yang di bawah parabola dan kedua yang dibawah parabola. Pada bagian yang diarsir kurva fx lebih di atas dibandingkan dengan kurva gx maka luas daerah di atas bisa dinyatakan dengan contoh soal 5. Tulisan ini terkait dengan tulisan. Luas daerah yang diarsir pada gambar di atas dapat dinyatakan dengan rumus. Hitunglah luas daerah yang dibatasi oleh garis y x.
Source: id.pinterest.com
Luas daerah yang dibatasi oleh kurva y x 2 4x 5 dan sumbu x adalah. Hitunglah luas daerah yang dibatasi oleh garis y x. Untuk itu kita harus menghitung 2 kali pertama yang di bawah parabola dan kedua yang dibawah parabola. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu y. Gunakan cara mirip cara di atas.
Menentukan luas daerah di bawah sumbu x. Misalkan persamaan garis kita tulis menjadi. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu y. Berdasarkan soal tersebut dapat kita lihat bahwa hanya terdapat satu titik potong yaitu.
Gunakan cara mirip cara di atas.
Agar kita dapat melihat perbedaan soal 1 dan soal 2. Integral Tak Tentu dan Luas Daerah. Contoh soal integral mencari luas daerah. Sumbu x berarti garis y 0.
Source: id.pinterest.com
Pada bagian yang diarsir kurva fx lebih di atas dibandingkan dengan kurva gx maka luas daerah di atas bisa dinyatakan dengan contoh soal 5. Pada soal 2 di atas persamaan parabola dan persamaan garisnya telah diketahui. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu Y. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu y.
Source: supermatematika.com
Integral banyak sekali penggunaanya seperti dalam menghitung luas daerah dibidang datar menggunakan integralmenghitung panjang busur menghitung luas selimut benda putar menghitung volume benda putar Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva di bawah kurva di atas sumbu x ataupun di bawah sumbu x. Fungsinya adalah y 4 - x2 rightarrow x sqrt4 - y. Daerah yang dibatasi oleh kurva yakar x dan garis x9 dibagi oleh garis xc c0 menjadi dua daerah dengan luas sama. Menentukan luas daerah di bawah sumbu x.
Source: teamhannamy.blogspot.com
Luas daerah yang dibatasi oleh kurva y x 2 4x 5 dan sumbu x adalah. Y 2x 5 dan sumbu x. L 10 3 10 3. Dengan demikian luasnya dapat ditentukan dengan menggunakan integral tentu berikut.
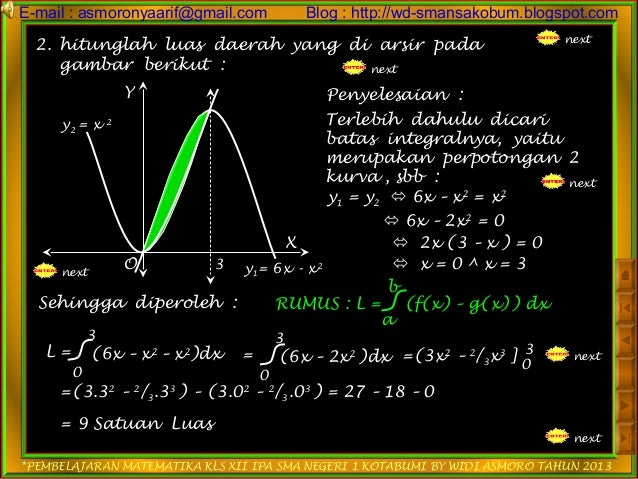
Perhatikan bahwa dari selang 0 4 kurva y 6 x x 2 selalu berada di atas kurva y x 2 2 x.
Perhatikan gambar di bawah. Hitunglah luas daerah yang dibatasi oleh garis y x. Daerah yang diarsir dibatasi oleh dua kurva parabola yaitu y x 2 2 x dan y 6 x x 2. Dengan menggunakan konsep yang sama kita bisa coba mengerjakan soal untuk mencari luas daerah dengan menggunakan integral tentu. Agar kita dapat melihat perbedaan soal 1 dan soal 2.
Source: id.pinterest.com
Perhatikan bahwa dari selang 0 4 kurva y 6 x x 2 selalu berada di atas kurva y x 2 2 x. Menentukan luas daerah di bawah sumbu x. Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva di bawah kurva di atas sumbu x ataupun di bawah sumbu x. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu y. Selanjutnya pembahasan tentang cara menghitung luas daerah kurva fungsi linear dengan sumbu x menggunakan integral tentu.
Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu y.
Rumus Cepat Menghitung Luas Daerah yang Dibatasi Kurva. Pada bagian yang diarsir kurva fx lebih di atas dibandingkan dengan kurva gx maka luas daerah di atas bisa dinyatakan dengan contoh soal 5. Kita akan coba untuk menghitung luas daerah dengan integral pada contoh soal nomor 5 di atas dengan batas yang kita gunakan ada pada sumbu Y. Batasnya adalah dari y 1 sampai y 4.
Source: teamhannamy.blogspot.com
Gunakan cara mirip cara di atas. Menentukan luas daerah di bawah sumbu x. Contoh soal integral mencari luas daerah. Y 2x 5 dan sumbu x.
Source: teamhannamy.blogspot.com
Fungsinya adalah y 4 - x2 rightarrow x sqrt4 - y. Perhatikan gambar di bawah. Setelah digambar grafiknya membentuk segitiga sehingga konsep menghitung dengan integral bisa diabaikan. Menentukan luas daerah di bawah sumbu x.
Source: teamhannamy.blogspot.com
Menentukan luas daerah di bawah sumbu x. Luas daerah yang dibatasi oleh kurva yx² dan garis xy6 adalah. Misalkan persamaan garis kita tulis menjadi. Luas daerahnya adalah 2 23 satuan luas.
Menentukan Batas Jika Diketahui Luasnya.
Y 2x 5 dan sumbu x. Untuk itu kita harus menghitung 2 kali pertama yang di bawah parabola dan kedua yang dibawah parabola. Karena luas harus bernilai positif maka rumus integral yang tepat untuk menghitung luas daerah tersebut adalah. Dengan demikian luasnya dapat ditentukan dengan menggunakan integral tentu berikut. Setelah digambar grafiknya membentuk segitiga sehingga konsep menghitung dengan integral bisa diabaikan.
Source: supermatematika.com
Menggunakan integral untuk mencari luas daerah yang dibatasi oleh dua kurvaCara cepatnya bisa dilihat di sinihttpsyoutubeoSmJaXXDTQE. Rumus Cepat Menghitung Luas Daerah yang Dibatasi Kurva. Misalkan persamaan garis kita tulis menjadi. Integral Tak Tentu dan Luas Daerah. Selanjutnya kita akan menghitung luas daerah tersebut dengan batas a 3 dan b 0.
Integral banyak sekali penggunaanya seperti dalam menghitung luas daerah dibidang datar menggunakan integralmenghitung panjang busur menghitung luas selimut benda putar menghitung volume benda putar Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva di bawah kurva di atas sumbu x ataupun di bawah sumbu x.
Batasnya adalah dari y 1 sampai y 4. Gunakan cara mirip cara di atas. Dengan menggunakan konsep yang sama kita bisa coba mengerjakan soal untuk mencari luas daerah dengan menggunakan integral tentu. Hitunglah luas daerah yang dibatasi oleh kurva y x - 2x dan sumbu x.
Source: encrypted-tbn0.gstatic.com
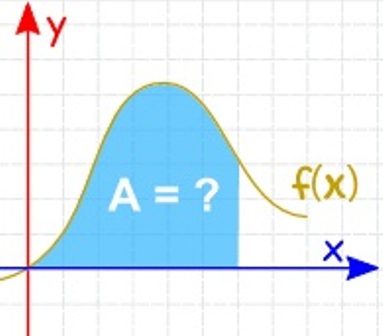
Integral Menghitung Luas Salah satu aplikasi integral tak tentu adalah untuk menghitung luas. Jadi luas daerahnya adalah 1 78 satuan luas. Sebuah daerah dibatasi oleh persamaan y 2 x dan y x 2. Y 2x 5 dan sumbu x. Integral banyak sekali penggunaanya seperti dalam menghitung luas daerah dibidang datar menggunakan integralmenghitung panjang busur menghitung luas selimut benda putar menghitung volume benda putar Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva di bawah kurva di atas sumbu x ataupun di bawah sumbu x.
Source: teamhannamy.blogspot.com
L 10 3 10 3. Selanjutnya kita akan menghitung luas daerah tersebut dengan batas a 3 dan b 0. Luas daerah yang dibatasi oleh kurva yx² dan garis xy6 adalah. Selanjutnya pembahasan tentang cara menghitung luas daerah kurva fungsi linear dengan sumbu x menggunakan integral tentu. Luas daerah yang dibatasi kurva y x2 3x y x 2 3 x sumbu-x x 0 x 0 dan x 2 x 2 adalah.
Source: madematika.net
Daerah yang dibatasi oleh kurva yakar x dan garis x9 dibagi oleh garis xc c0 menjadi dua daerah dengan luas sama. Luas daerah yang dibatasi oleh kurva yx² dan garis xy6 adalah. Luas daerah yang dibatasi oleh kurva y x 2 4x 5 dan sumbu x adalah. Selanjutnya kita akan menghitung luas daerah tersebut dengan batas a 3 dan b 0. Luas daerah yang dibatasi oleh garis x 3y 4 sumbu x untuk 1 x.
Situs ini adalah komunitas terbuka bagi pengguna untuk berbagi apa yang mereka cari di internet, semua konten atau gambar di situs web ini hanya untuk penggunaan pribadi, sangat dilarang untuk menggunakan artikel ini untuk tujuan komersial, jika Anda adalah penulisnya dan menemukan gambar ini dibagikan tanpa izin Anda, silakan ajukan laporan DMCA kepada Kami.
Jika Anda menemukan situs ini bagus, tolong dukung kami dengan membagikan postingan ini ke akun media sosial seperti Facebook, Instagram dan sebagainya atau bisa juga save halaman blog ini dengan judul contoh soal integral tentu menghitung luas daerah dengan menggunakan Ctrl + D untuk perangkat laptop dengan sistem operasi Windows atau Command + D untuk laptop dengan sistem operasi Apple. Jika Anda menggunakan smartphone, Anda juga dapat menggunakan menu laci dari browser yang Anda gunakan. Baik itu sistem operasi Windows, Mac, iOS, atau Android, Anda tetap dapat menandai situs web ini.
